DFS-基础
DFS简介
- 搜索:穷举问题解空间的部分/所有解,从而求出问题的解
- 深度优先搜索:尽可能一条路走到底,走不通了再回退
n重循环
本质上就是暴力,呈现出一种树状结构。n重循环就是n层的树
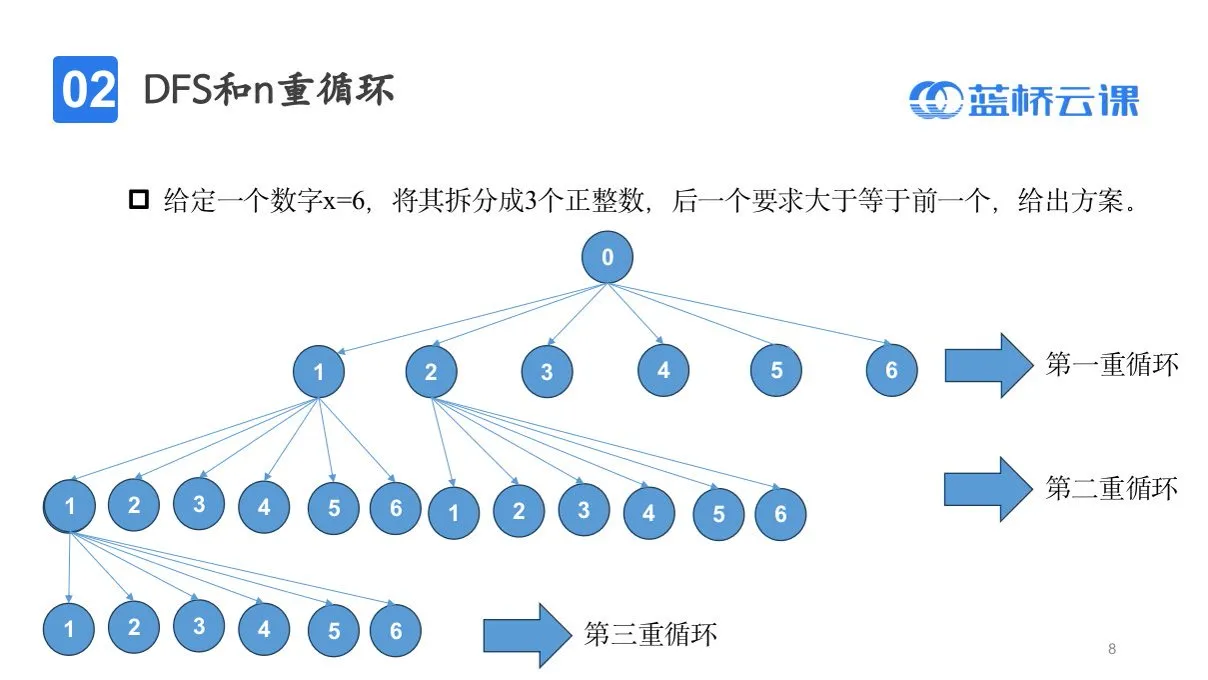
大致的模板:

模板题目如下:
x = int(input())
n = int(input())
path = [0]*n
#depth:当前处于第几层
def dfs(depth):
#递归出口
if depth == n:
#条件判断
for i in range(1,n):
if path[i] < path[i-1]:
return
if sum(path) != x:
return
print(path)
return
#对于每一层枚举当前拆出来的数字
for i in range(1,x+1):
#记录当前层
path[depth] = i
dfs(depth+1)
#对应递归出口,看你的习惯
dfs(0)有的搜索确实没必要或者优化,剪枝详细讲!优化如下:
x = int(input())
n = int(input())
path = [0]*n
#depth:当前处于第几层
def dfs(depth,last_value):
#递归出口
if depth == n:
#就不需要判断递增性
if sum(path) != x:
return
print(path)
return
#对于每一层枚举当前拆出来的数字
for i in range(last_value,x+1):
#记录当前层
path[depth] = i
dfs(depth+1,i)
#对应递归出口,看你的习惯
dfs(0,1)例题:分糖果
跟之前的不同之处就在于两种糖果怎么体现出不同,方法就是用两个循环去枚举。思路还是枚举7个小朋友,循环7次。
例题:买瓜
莫名其妙在蓝桥杯官网找不到这个题了。
思路
- 对于一个瓜来说有三种可能:0,一半,全买了;
- 用乘2倍的方式避免小数。
import sys
input = lambda:sys.stdin.readline().strip()
n,m = map(int , input().split())
#避免小数
m *= 2
w1 = list(map(int ,input().split()))
w = [x*2 for x in w1]
ans = -1
def dfs(depth,sum,count):
#剪枝,已经不合法,没必要进行下去
if sum > m:
return
if sum == m:
global ans
ans = max(ans,count)
if depth == n:
return
#不买
dfs(depth+1,sum,count)
#买一半
dfs(depth+1,sum+w[depth]//2,count+1)
#全买
dfs(depth+1,sum+w[depth],count)
dfs(0,0,0)
print(ans)超时是搜索的宿命(抽烟)。放宽心吧我只能说。

DFS-回溯
是什么?
DFS的一种,用到了剪枝的技巧。强调走过的路打标记。
- 排列树
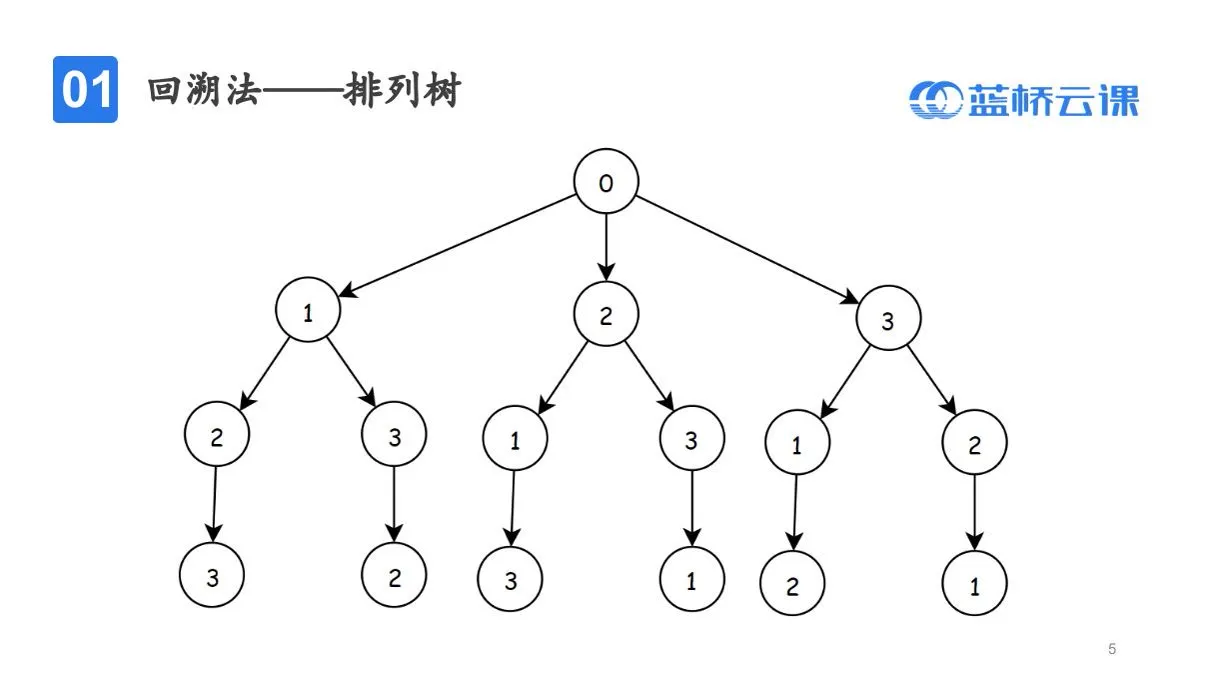
- 子集树
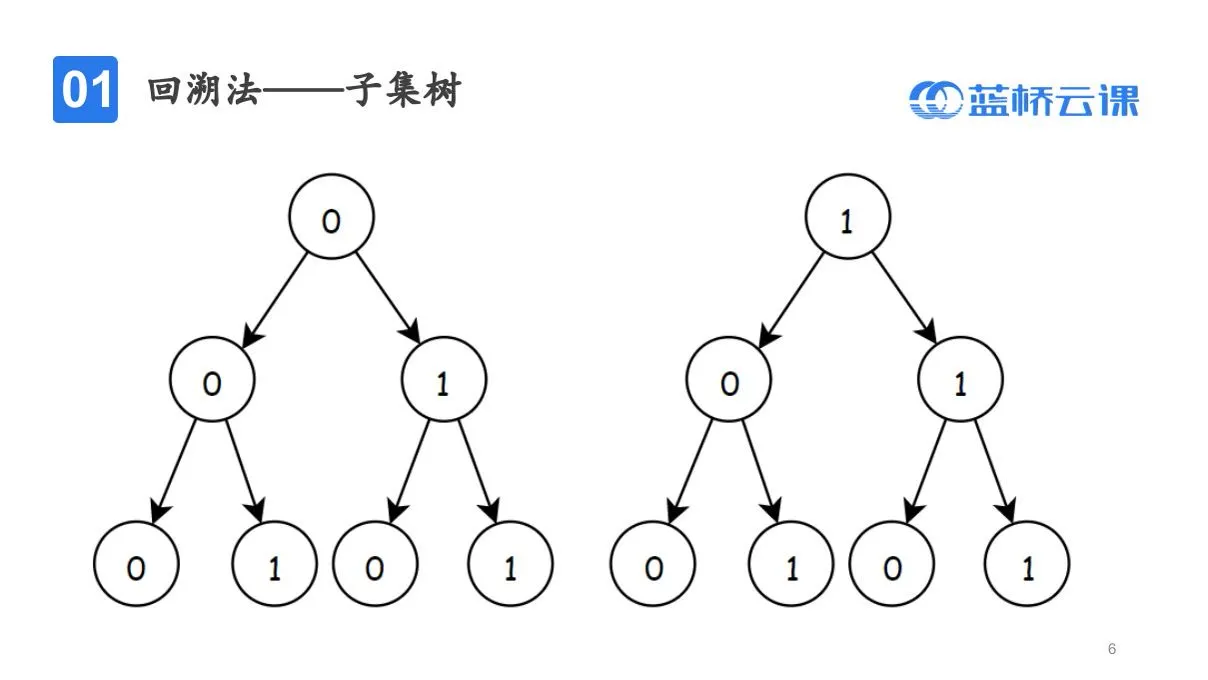
回溯模板
- 每次选择的数字打标记——vis数组;
- 记录路径——path数组;
- 回溯总流程:打标机-记录路径-下一层-回到上一层-清楚标记
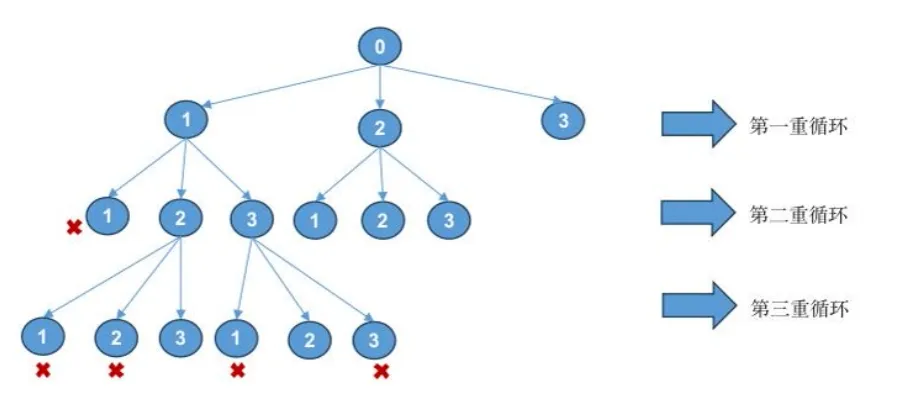
排列模板题
import sys
input = lambda:sys.stdin.readline().strip()
def dfs(depth):
#回到上一层
if depth == n:
print(path)
return
for i in range(1,n+1):
#未标记数字
if vis[i]:
continue
#打表记
vis[i] = True
#记录路径
path.append(i)
#下一层
dfs(depth+1)
#消除标记
vis[i] = False
path.pop(-1) #弹出列表最后一个元素
n = int(input())
vis = [False] * (n+1)
path = []
dfs(0)输入3可以得到:
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]子集模板题
import sys
input = lambda:sys.stdin.readline().strip()
def dfs(depth):
#回到上一层
if depth == n:
print(path)
return
#不需要用vis进行标记
#选择该数字
path.append(ls[depth])
dfs(depth+1)
path.pop(-1)
#不选择该数字
dfs(depth+1)
n = int(input())
ls = list(map(int , input().split()))
vis = [False] * (n+1)
path = []
dfs(0)输入:
3
1 2 3得到输入:
[1, 2, 3]
[1, 2]
[1, 3]
[1]
[2, 3]
[2]
[3]
[]例题:N皇后
不知道干嘛,这个题也没了。读了一下题目,感觉是有点歧义。探究一下如何保证两条对角线上面没有皇后。
- 从左上到右下

可以看到,同一对角线上的(x,y)差值一定。从(1,1)开始,x-y的范围为[-N+1,N-1],因此对于N*N的图像,总共有(2*N - 1)条对角线。
- 从左下到右上

可以看到,同一对角线上的(x,y)和值一定。从(1,1)开始,x+y的范围为[2,2*N],因此对于N*N的图像,总共有(2*N - 1)条对角线。
import sys
input = lambda:sys.stdin.readline().strip()
cnt = 0
def dfs(depth):
#第depth层的皇后,保证一行只有一个皇后
if depth == n+1:
global cnt
cnt += 1
return
for y in range(1,n+1):
if vis1[y] is False and vis2[depth-y+n] is False and vis3[depth+y] is False:
#打标记
vis1[y] = vis2[depth-y+n] = vis3[depth+y] = True
#下一层
dfs(depth+1)
#清空标记
vis1[y] = vis2[depth-y+n] = vis3[depth+y] = False
n = int(input())
#一以下就是剪枝
#保证列
vis1 = [False] * (n+1)
#差的范围为[-N+1,N-1]
vis2 = [False] * (2*n+1)
#和的范围为[2,2N]
vis3 = [False] * (2*n+1)
dfs(1)
print(cnt)例题:小朋友崇拜圈
说明搜索不仅能用在n重循环中,还可以用在图论上。
思路
- 标记每个走过的点,走到一个走过的地方就停;
- 环长计算:对同一个点,两个length相减。
同时,预估一下递归层数,可以对它进行扩大。
import sys
#增加深度
sys.setrecursionlimit(100000)
input = lambda:sys.stdin.readline().strip()
n = int(input())
ls = [0] + list(map(int , input().split()))
ans = 0
def dfs(x,length):
#x是第几个小朋友,length是走的步数
if vis[x] != -1:
global ans
ans = max(ans,length - vis[x])
return
#标记
vis[x] = length
dfs(ls[x],length+1)
#直接用vis记录步长就行,同时可以作为是否已经遍历过的依据
vis = [-1] * (n+1)
#找到不同的圆
for i in range(1,n+1):
if vis[i] == -1:
dfs(i,0)
print(ans)例题:全球变暖
题意有一些难理解,但是本质上就是找有几块这样的地,上下左右都是’#‘。所以这个题目其实需要分成两个步骤:
- 统计有多少个岛屿;
- 统计岛屿里面是否有上下左右都是’#‘的地,如果有就不会被完全淹没。
import sys
sys.setrecursionlimit(100000)
input = lambda:sys.stdin.readline().strip()
n = int(input())
ls=[]
for i in range(n):
ls.append(list(input()))
#注意这里的位置变换啊啊啊啊,不要想当然
d = [(-1,0),(1,0),(0,-1),(0,1)]
ans = 0
def dfs(x,y):
vis[x][y] = 1
count = 0
for dx,dy in d:
if 0 <= x+dx <n and 0 <= y+dy <n:
#周围是陆地
if ls[x+dx][y+dy] == '#':
count += 1
#没有遍历过
if vis[x+dx][y+dy] == 0:
dfs(x+dx,y+dy)
if count == 4:
global f
f = 1
return
vis = [[0]*n for i in range(n)]
for i in range(n):
for j in range(n):
if vis[i][j] == 0 and ls[i][j] == '#':
#当前岛屿是否存在标记
f = 0
dfs(i,j)
#注意这是没有高地才加一
if f == 0:
ans += 1
print(ans)很漂亮(大哭)
DFS-剪枝
是什么?
根据当前状态判断后续无解,可以及时停止。
eg.N个正整数有多少个子集之和小于等于K。前面几个数如果达到了K,就可以及时停止。
分类
- 可行性剪枝:状态与题意不符。例如:排列;
- 最优性剪枝:当前状态不如最优解。例如:最小值。
例题:数字王国之军训排队
啊啊啊这个自己写对了啊啊啊啊
import sys
input = lambda:sys.stdin.readline().strip()
n = int(input())
ls = list(map(int,input().split()))
ans = n
def check(l,x):
for i in l:
if i % x == 0 or x % i == 0:
return False
return True
def dfs(depth):
if depth == n:
global ans
ans = min(ans,len(teams))
return
for i in range(len(teams)):
if check(teams[i],ls[depth]):
teams[i].append(ls[depth])
dfs(depth+1)
teams[i].pop(-1)
new = [ls[depth]]
teams.append(new)
dfs(depth+1)
teams.pop(-1)
teams = []
dfs(0)
print(ans)例题:特殊的多边形
我感觉比较不清楚的是,怎么保证能够组成一个多边形。例如三角形,1、2、3就无法构成。但是这完全就是数学知识了:
任意N-1条边之和大于第N条边,可以构成N边形。要注意的是,这里验证N变形不需要验证i边形成立,只需要最后递归出口的地方验证一下就行。
预处理(打表)+前缀和求解答案
import sys
input = lambda:sys.stdin.readline().strip()
t,n = map(int ,input().split())
r_max = 0
l_min = 100000
ls = []
for i in range(t):
l,r = map(int , input().split())
l_min = min(l_min,l)
r_max = max(r_max,r)
ls.append((l,r))
#用单增进行优化
def dfs(depth,last_num,k):
if depth == n:
if sum(path) <= 2*last_num:
return
vis[k] += 1
return
for i in range(last_num+1,r_max):
#剪枝
if k * (i ** (n - depth)) > r_max:
return
path.append(i)
dfs(depth+1,i,k * i)
path.pop(-1)
vis = [0] * 100001
path = []
#类似地,这里也不要想当然,边长是可以等于1的
dfs(0,0,1)
for i in range(1,len(vis)): #构造前缀和数组
vis[i] += vis[i-1]
for l,r in ls:
print(vis[r] - vis[l-1])记忆化搜索
是什么?
通过记录已经遍历过的状态的信息,避免对同一状态的重复遍历
记忆化 = dfs + 额外字典
例题:斐波拉契数列
求f(n),对1e9+7取模
import sys
input = lambda:sys.stdin.readline().strip()
sys.setrecursionlimit(100000)
dic = {0:1,1:1}
def f(n):
if n in dic.keys():
return dic[n]
dic[n] = (f(n-1)+f(n-2))%1000000007
return dic[n]
n = int(input())
print(f(n))卧槽python你个老六你他妈又写好了
from functools import lru_cache
#直接把普通递归变成记忆化递归
@lru_cache(maxsize=None)
#不用改动原本的递归函数
def f(n):
if n == 0 or n == 1:
return 1
else:
return f(n-1)+f(n-2)
n = int(input())
print(f(n))例题:混境之地5
其实我感觉这个题目最重要的教训在于map本身就是一个关键词,最好还是不要作为变量。遇到那种list object is not callable的错误要考虑这种关键词用作变量名称的可能。
#因为先往下,再往右和线往右再往下的结果是一样的,所以可以用记忆化搜索的方式
from functools import lru_cache
@lru_cache(maxsize = None)
def dfs(x,y,z):
#到达终点
if x == c-1 and y == d-1:
return True
for dx,dy in [(-1,0),(1,0),(0,-1),(0,1)]:
xx = x+dx
yy = y+dy
if xx < 0 or xx >= n or yy < 0 or yy >=m:
continue
#新坐标比旧坐标低,能够走到新坐标
if Map[xx][yy] < Map[x][y]:
if dfs(xx,yy,z):
return True
#可以用喷气背包
elif Map[xx][yy] < Map[x][y] + k and z==False:
if dfs(xx,yy,True):
return True
n,m,k = map(int , input().split())
a,b,c,d = map(int , input().split())
Map = []
for i in range(n):
Map.append(list(map(int , input().split())))
if dfs(a-1,b-1,False):
print("Yes")
else:
print("No")例题:地宫寻宝
这个题目相比于之前就是对运动方向进行了严格限定。遇到了之前就比较常见的问题,一个题目没有想清楚函数是处理当前状态还是下一状态的时候,脑子里突然乱掉了。学习这道题的处理方法吧!
import sys
from functools import lru_cache
sys.setrecursionlimit(100000)
input = lambda:sys.stdin.readline().strip()
n,m,k = map(int,input().split())
Map = []
#当前坐标,之前的宝物数量与最大值
@lru_cache(maxsize = None)
def dfs(x,y,sum_num,max_num):
#递归出口
if x == n-1 and y == m-1:
if sum_num == k:
return 1
if sum_num == k-1 and max_num < Map[x][y]:
return 1
return 0
ans = 0
#方案数 = 右边的方案数 + 下面的方案数
for dx , dy in [(1,0),(0,1)]:
xx = x+dx
yy = y+dy
if xx < 0 or xx >= n or yy < 0 or yy >= m:
continue
#当前不选择宝物,走到(xx,yy)
ans += dfs(xx,yy,sum_num,max_num)
#当前选择宝物,走到(xx,yy)
#注意这里是准备拿现在的宝物
if max_num < Map[x][y]:
ans += dfs(xx,yy,sum_num+1,Map[x][y])
ans %= 1000000007
return ans
for i in range(n):
Map.append(list(map(int , input().split())))
print(dfs(0,0,0,-1))完结撒花!

