前缀和算法!启动!
有一阵子荒废了,昨天发烧+感冒确实是遭老罪,除了浑身没力气,消化功能也变差了很多很多。明天早上还是要喝点粥过渡一下,不要不吃早饭了。
今天开始写博客之前用打算用Haroopad打开md文件,结果等了很久都没打开,莫名其妙的,又不想再下载其他软件了,以后都直接用vscode的插件。所以程序员的尽头就是vscode()。
二维前缀和
二维前缀和的定义
sum(x,y):从下标(0,0)到(x, y)子矩阵内元素的和【默认从(0,0)开始】。例如:sum(2,3)图示:
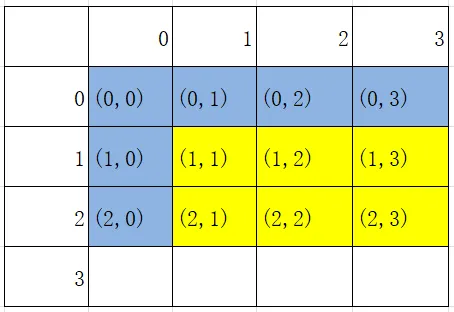
为什么图中有一部分是标记为蓝色呢?要注意回顾,之前一维前缀和我们代码中有一句:
#前缀和列表,注意这里有个添加0的处理
s = list(chain([0],list(accumulate(ls))))在二维中也是一样,我们的数值是从(1,1)开始有定义的,(x,0)与(0,x)都默认为0。
二维前缀和递推公式
之前一维的递推公式:
sum[i] = sum[i-1] + num[i]结合经验,我们考虑x、y两个维度上面都减一,发现有面积重叠的部分,如图所示:

因此我们也得到了最终的递推结论:
sum[x][y] = sum[x-1][y] + sum[x][y-1] + num[x][y] - sum[x-1][y-1]子矩阵求法
在前缀和的基础之上的一个应用,就是“开始点”不是(0,0)的时候可以怎么做。我们依旧用图像来理解:
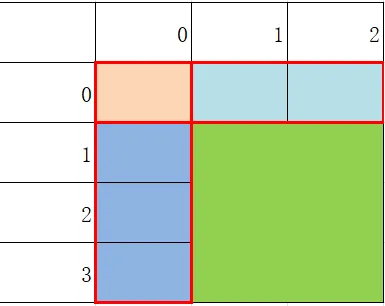
类似地,用两块长条减去重叠的部分,得到的结果再与前缀和相减就行。注意图示是一种特殊情况(正好重叠部分只有(0,0)一个点)
我们可以得到公式:要求出(x1,y1)到(x2,y2)之间的数的和(x1 < x2 , y1 < y2):
sum = sum[x2][y2] - (sum[x1][y2] + sum[x2][y1] - sum[x1][y1])
=sum[x2][y2] + sum[x1][y1] - sum[x1][y2] - sum[x2][y1]例题:P1387 最大正方形
这道题tag居然有dp,但是稍微一想确实有点像,但是这个题目与传统的dp直接输出dp[n][m]也并不相同。没错,本人就是在这个死胡同上栽了跟头。
我们用dp[i][j]定义的是每个位置为右下角的最大正方形的边长。递推的本质是你要去拓展,如果你在(x,y)点想要拓展正方形的边长,那你就得要求,首先它本身是1,其次它的左上三个点的位置的dp足够长。如果它本身就是0,那么就不可能构成正方形。有以下状态转移方程:
if num[i][j] == 1:
dp[i][j] = min(dp[i−1][j],dp[i][j−1],dp[i−1][j−1])+1
else:
dp[i][j] = 0所以说前缀和其实也算是动态规划常用到的工具,学习的顺序还是反了啊(冒汗)。
以下是编程实现:
import sys
input = lambda: sys.stdin.readline().rstrip()
#数列表是从0开始的,dp列表是从(1,1)开始的
n,m = map(int, input().split())
a = []
for i in range(n):
a.append(list(map(int, input().split())))
dp = [[0] * (m+1) for _ in range(n+1)]
ans = 0
for i in range(n):
for j in range(m):
if a[i][j] == 0:
dp[i+1][j+1] = 0
else:
dp[i+1][j+1] = min(dp[i][j+1], dp[i+1][j], dp[i][j])+1
ans = max(ans, dp[i+1][j+1])
print(ans)在洛谷上发现一开始下标并没有设置好,结果全AC了,在题解里面也看到说这道题用搜索、二分、暴力都行。emmm仁者见仁智者见智吧。
后缀和
后缀和的定义基本上就是和前缀和颠倒过来,只是在处理时,首先要将数列表倒置,acculate一下,然后再把求和也导致,处理起来才比较方便。可以用于做下面的经典例题:
寻找数组的中心下标
但是本人并不刷力扣(好吧是因为涉及到面向对象本人不会),所以就用一下案例检验,不提交检查了。
案例输入如下:
#表示输入数字的个数
6
1 7 3 6 5 6输出如下:
3解释:
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。代码如下:
from itertools import *
import sys
input = lambda: sys.stdin.readline().rstrip()
n = int(input())
ls = list(map(int, input().split()))
#前缀和
acc = list(accumulate(ls))
sum1 = list(chain([0],acc))
#后缀和
ls.reverse() #没有返回值
acc = list(accumulate(ls))
sum2 = list(chain([0],acc))
sum2.reverse() #貌似这样做下标处理更方便
f=0
for i in range(n):
if sum1[i]== sum2[i+1]:
f=1
print(i)
break
if f==0:
print(-1)树上前缀和(前缀树/字典树)
参考资料:
前缀树的定义
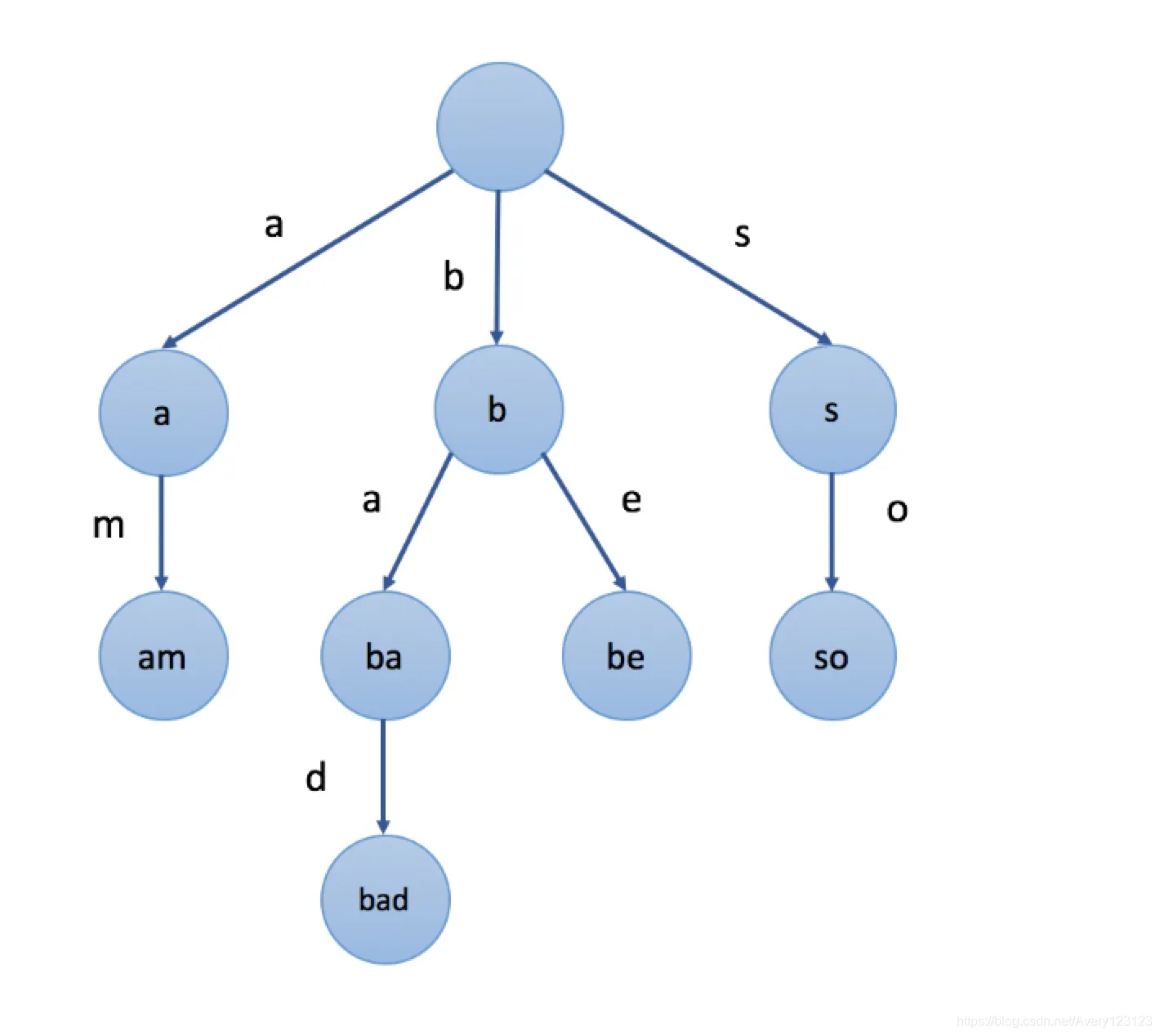
如图所示,通常来说,一个前缀树是用来存储字符串的。前缀树的每一个节点由通往该节点的路径上的字符组成。
前缀树的一个重要的特性是,节点所有的后代都与该节点相关的字符串有着共同的前缀。这就是前缀树名称的由来。
前缀树基本操作
插入操作/构建操作
构建前缀树实际上就是初始化根节点+多次调用插入函数,所以这里就讲一下插入函数的思路。
具体地说,如果我们在前缀树中插入一个字符串S,遍历字符串的每一个字符,从根节点开始,看是否存在该字符,来决定选择一个子节点或添加一个新的子节点,然后移动遍历的对象。
搜索操作
- 搜索前缀
从前缀和的定义,我们可以衍生出一种题型:搜索以特定前缀开头的任何单词。
思路与之前一致,沿着树往下搜索就行,如果在前缀未完成搜索之前就已经没有字节点了,说明就没有以该前缀开头的单词。
- 搜索单词
类似于前缀,先把它当作一个前缀进行搜索,如果搜索成功,还需要对它是否只是一个前缀进行判断,树的结构上面需要一些调整。
前缀树的Python实现
很痛苦啊但是B组就有这个要求,但是我没学好类啊啊啊……学吧孩子们。博客上面的我没有看懂,就直接用leetcode上面模板题的题解来进行理解好了。但是这也给我提供了一个很好的学习平台的思路啊leetcode,我确实对你开发太少了。
class Trie:
def __init__(self):
#说实话是对数据结构要求最低的一种方法了,用列表模拟的
self.children = [None] * 26 #至多只能有26个字节点,需要提前开辟空间,注意中间的None
self.isEnd = False #是不是本身单独也是一个单词
def searchPrefix(self, prefix: str) -> "Trie":
node = self #从根节点开始
for ch in prefix:
ch = ord(ch) - ord("a")
if not node.children[ch]:
return None #前缀无法遍历完,直接返回None
node = node.children[ch]
return node #前缀能够遍历完
def insert(self, word: str) -> None:
node = self #从根节点开始
for ch in word:
#将一个小写字母字符转换为其在字母表中的相对位置索引(从0开始)
ch = ord(ch) - ord("a")
if not node.children[ch]:
node.children[ch] = Trie()
node = node.children[ch] #指向下一个字符对应的子节点
node.isEnd = True #标记为可以组成一个单词
#查找单词是否存在
def search(self, word: str) -> bool:
node = self.searchPrefix(word)
return node is not None and node.isEnd #前缀能够遍历完并且node是一个单独的单词才返回True
#查找前缀是否存在
def startsWith(self, prefix: str) -> bool:
return self.searchPrefix(prefix) is not None理解了以上模板之后,我们解决一下问题
单词的压缩编码
这个题目我们重点要理解一下第一个输出示例:
输入:words = ["time", "me", "bell"]
输出:10
解释:一组有效编码为 s = "time#bell#" 和 indices = [0, 2, 5] 。
words[0] = "time",s 开始于 indices[0] = 0 到下一个 '#' 结束的子字符串;
words[1] = "me",s 开始于 indices[1] = 2 到下一个 '#' 结束的子字符串;
words[2] = "bell" ,s 开始于 indices[2] = 5 到下一个 '#' 结束的子字符串。对于me,可以看到它的前缀是没有“#”来标记的,这种就叫作后缀单词。在该题中,后缀单词是否存在是不影响最终结果的。比方说我们再加一个单词’ime’,最终编码依旧是”time#bell#“。要保证后缀单词对结果没有影响,我们必须要求后缀单词在完整单词的后面。因此一开始我们就要对单词列表按照字符串长度进行排序。在这路我们用到sort()函数:
list.sort(cmp=None, key=None, reverse=False)对于其中的参数:
| 参数 | 功能 |
|---|---|
| cmp | 可选参数,用于排序的方法 |
| key | 可选参数,用来进行比较的元素,指定可迭代对象中的一个元素来进行排序 |
| reverse | 排序规则,True降序,False升序,默认升序 |
对于后缀的处理,我们可以跟之前一样,整体构造一个后缀树,此时后缀单词就变成了前缀,对模板的修改就减少了很多。
我们对这个题目做一点改变(改成oi的模样):
输入:
3
time
me
bell输出:
time#bell#编程实现:
import sys
class Trie:
def __init__(self):
self.children = [None] * 26
self.isEnd = False # 是不是本身单独也是一个单词
def searchPrefix(self, prefix: str) -> "Trie":
node = self # 从根节点开始
for ch in prefix:
ch = ord(ch) - ord("a")
if not node.children[ch]:
return None # 前缀无法遍历完,直接返回None
node = node.children[ch]
return node # 前缀能够遍历完
def insert(self, word: str) -> None:
node = self # 从根节点开始
for ch in word:
# 将一个小写字母字符转换为其在字母表中的相对位置索引(从0开始)
ch = ord(ch) - ord("a")
if not node.children[ch]:
node.children[ch] = Trie()
node = node.children[ch] # 指向下一个字符对应的子节点
node.isEnd = True # 标记为可以组成一个单词
# 查找前缀是否存在
def startsWith(self, prefix: str) -> bool:
return self.searchPrefix(prefix) is not None
input = lambda: sys.stdin.readline().strip()
n = int(input())
words = []
line = ""
for i in range(n):
#把单词逆序
x=input()
x=x[::-1]
words.append(x)
words.sort(key=len, reverse=True)
trie = Trie()
for word in words:
if trie.startsWith(word) == False:
trie.insert(word)
#记得把单词转回来
word = word[::-1]
line += (word+'#')
print(line)运行起来是有点子不快的……但是很难得做出来了,感觉是没有什么特别复杂的地方,处理起来为啥太慢了我也要想想……这一篇先到这里吧,差分后面再说。

