枚举
是什么?
- 逐个尝试所有可能的值或组合来解决问题
- 问题空间必须是离散的
具体步骤
- 确定解空间:一维?二维?;
- 确定空间边界:最值、步长;
- 估算时间复杂度,优化。
例题:百钱买百鸡

- 思路一:枚举三种鸡的数量
公鸡上限:100 // 5 = 20
母鸡上限:100 // 3 = 33
小鸡上限:100 * 3 = 300 > 100,可以限定上线为100
时间复杂度:20*33*100
- 思路二:枚举两个变量
假设枚举公鸡为x只,母鸡为y只
小鸡用的钱:(100 - 5x - 3y)
小鸡的数量:3(100 - 5x - 3y)
时间复杂度:20*33
- 思路三:枚举一个变量,后面两个变量通过二元一次方程组求解
时间复杂度:20
例题:字符计数
没有什么特别能说的,主要就是记得,判断字符是否在字符串中可以直接用if c in 字符串,不用把字符串转成列表。
例题:反倍数
记录一个课上的笔记:容斥原理
- [1,n]中a的倍数个数:n // a;
- [1,n]中b的倍数个数:n // b;
- [1,n]中ab的倍数个数:n // ab;
- [1,n]中a的倍数或者b的倍数个数:n // a + n // b - n // ab;
模拟
含义
直接按照题目含义模拟
注意事项
- 读懂题目;
- 步骤与代码一一对应;
- 提取重复部分,写成对应函数;
- 分块调试。
例题:饮料换购
编程实现:
import sys
input = lambda:sys.stdin.readline().strip()
n = int(input())
sum = n
f = 0
while n != 0:
f+=1
n-=1
if f==3:
f=0
n+=1
sum+=1
print(sum)老师讲的减少循环的方法:
#n:瓶盖数
#ans:饮料
n = int(input())
ans = n
while True:
if n>=3:
#把三个瓶盖换成一瓶饮料
n-=3
#统计饮料
ans += 1
#更新瓶盖
n += 1
else:
break
print(ans)优化:
#n:瓶盖数
#ans:饮料
n = int(input())
ans = n
while True:
if n>=3:
#n个瓶盖可以换n//3个饮料,剩余n%3
#统计饮料
ans += n // 3
#更新瓶盖
n = n%3 + n//3
else:
break
print(ans)例题:图像模糊
可以用之前扫雷一样的,用dir记录偏移值。也可以用一个双重循环,跟遍历dir的循环次数是一样的。
一个比较不好的习惯就是变量重复定义,导致很难找的错误。
编程实现:
import sys
input = lambda:sys.stdin.readline().strip()
n,m = map(int , input().split())
num = []
for i in range(n):
ls = list(map(int , input().split()))
num.append(ls)
#ls为二维数组
ans = [[0] * m for _ in range(n)]
#dir = [(-1,-1),(-1,0),(-1,1),(0,-1),(0,0),(0,1),(1,-1),(1,0),(1,1)]
for i in range(n):
for j in range(m):
sum = 0
count = 0
#遍历每个位置求结果
for dx in [-1,0,1]:
for dy in [-1,0,1]:
#和dir一样的效果
x = i + dx
y = j + dy
if 0 <= x < n and 0 <= y < m:
sum+=num[x][y]
count += 1
ans[i][j] = sum // count
for a in ans:
print(" ".join(map(str,a)))例题:螺旋矩阵
模拟行进过程
# 第一步
x,y=0,0
value = 1
num[x][y] = value
while value < n * m:
#不断向右走,保证下一个点不越界、没数字
while y+1 < m and num[x][y+1] == 0:
value += 1
y += 1
num[x][y] = value
#不断向下走,保证下一个点不越界、没数字
while x+1 < n and num[x+1][y] == 0:
value += 1
x += 1
num[x][y] = value
#不断向左走,保证下一个点不越界、没数字
while y - 1 >= 0 and num[x][y-1] == 0:
value += 1
y -= 1
num[x][y] = value
#不断向上走,保证下一个点不越界、没数字
while x - 1 >= 0 and num[x-1][y] == 0:
value += 1
x -= 1
num[x][y] = value拓展:横折的方式
1 2 6 7
3 5 8 13
4 9 12 14
10 11 15 16
递归
是什么?
通过自己调用自己来解决问题的函数。通常把大型复杂问题层层转化为一个与原问题相似的、规模较小的问题求解。
注意事项
- 递归出口
- 如何化成子问题
同时可以作为函数的书写顺序。
快速排序
采用递归实现,时间复杂度为O(n)。
# 快速选择算法,找第k小的数字,假设可能存在数字相同
# 例如:3,2,1,5,6,4。k=2
#(1)3为基准,变成【1,2】,【3】,【5,6,4】
# len(left)=2,len(middle)=1,k<=len(left),在左边的子列表中
#(2)1为基准,变成【1】,【2】
# len(left)=0,len(middle)=1,k>len(left) and k>len(left)+len(right),说明在右边的子列表中
#(3)右列表中只有一个元素,返回这个元素
# 例如:3,2,1,5,6,4。k=3
#(1)3为基准,变成【1,2】,【3】,【5,6,4】
# len(left)=2,len(middle)=1,k>len(left) and k<=len(left)+len(middle),说明在中间的子列表中
# 要注意,中间列表所有的数字都是一样的,所以直接返回基准值就行
# 例如:3,2,1,5,6,4。k=4
#(1)3为基准,变成【1,2】,【3】,【5,6,4】
# len(left)=2,len(middle)=1,k>len(left) and k<=len(left)+len(middle),说明在右边的子列表中
#(2)5为基准,变成【4】,【5】,【6】
# 此时k要更新为k - len(left) - len(middle),在递归之前更新,即k=4-1-2=1
# len(left)=1,len(middle)=1,k<=len(left),说明在左边的子列表中
#(3)左列表中只有一个元素,返回这个元素
import sys
input = lambda:sys.stdin.readline().strip()
def QuickSearch(ls,k):
#递归终点:所在的区间只有一个元素
if len(ls) == 1:
return ls[0]
num = ls[0]
#划分列表
left = [x for x in ls if x < num]
middle = [x for x in ls if x == num]
right = [x for x in ls if x > num]
left_count = len(left)
middle_count = len(middle)
if k <= left_count:
return QuickSearch(left,k)
elif k<=left_count+middle_count:
return num
else:
return QuickSearch(right,k-left_count-middle_count)
k = int(input())
ls = list(map(int , input().split()))
print(QuickSearch(ls,k))
进制转换
感觉学一下这个列表和字典的使用比较有用。从中必须学习到一个函数enumerate().
enumerate()函数
用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列,同时列出数据和数据下标.
语法如下:start表示起始下标
enumerate(sequence,[start=0])直观地看一下效果:
ls = ['jvm','jre','javase']
print(list(enumerate(ls))) #注意转换成list类型得到输出结果:
[(0, 'jvm'), (1, 'jre'), (2, 'javase')]具体在for循环中使用的时候,可以直接用两个变量去对应达到序号和对应值。不需要加上list。
int_to_char = '0123456789ABCDEF'
char_to_int={}
for idx , chr in enumerate(int_to_char):
char_to_int[chr] = idx前缀和
这一部分自己学过了,主要是做一下课上的题目,同时复习一下迭代器的使用。要注意的点:
- 如果提前对所有数字进行取模,相减的时候下标大的数字可能比下标小的要小,记得加个MOD;
- 如何处理每个数字的不同次方?
例题:区间次方和
import sys
from itertools import *
MOD = 1000000007
input = lambda:sys.stdin.readline().strip()
n,m = map(int , input().split())
#注意extend的使用方法
a = [0]
a.extend(list(map(int , input().split())))
#提前准备不同次方的前缀和,注意到题干中k在[1,5]之间的范围
sum_ls =[[]]
for i in range(1,6):
tmp = [x ** i for x in a]
tmp_sum = list(accumulate(tmp))
tmp_sum = [x % MOD for x in tmp_sum]
sum_ls.append(tmp_sum)
for i in range(m):
l,r,k= map(int , input().split())
print((sum_ls[k][r] - sum_ls[k][l-1] + MOD) % MOD)
例题:小郑的蓝桥平衡串
这个看起来不错哈,有点那味了,不说我真看不出来是前缀和。我的初步设想是,用两个列表分别存储L和Q从下标0到改下标的数量。因为求最长平衡串,所以从整个字符串的长度开始,使用两个“指针”,每次长度减一进行遍历,遇到符合平衡就是最长的。
与老师讲的区别:
- 优化一下空间:L标注为1,Q标注为-1,相加为0就说明抵消了;
- 不要用两个指针的方式,直接枚举,时间复杂度能过。自己误写的两个指针的代码完全是错的。
代码实现如下:
import sys
from itertools import *
input = lambda:sys.stdin.readline().strip()
line = input()
a = [0]
for c in line:
if c=='L':
a.append(1)
else:
a.append(-1)
num = list(accumulate(a))
length = len(line)
ans = 0
for i in range(length):
for j in range(length,i,-1):
if num[j] - num[i] == 0:
ans = max(ans,j-i)
print(ans)
写的时候就要时刻注意,在开头要不要加0,加了0之后会有什么效果,注意print模拟一下保过。
例题:统计子矩阵
import sys
input = lambda:sys.stdin.readline().strip()
n,m,k = map(int,input().split())
#注意下标从1开始
num = [[0] * (m+1) for i in range(n+1)]
sum= [[0] * (m+1) for i in range(n+1)]
t = 0
for i in range(1,n+1):
#num[i]表示一行数组
num[i] = [0] + list(map(int,input().split()))
#预处理从行或者从列开始都行,习惯上按行处理
for i in range(1,n+1):
for j in range(1,m+1):
sum[i][j] = num[i][j] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1]
'''检验
for i in range(1,1+n):
print(" ".join(map(str,sum[i][1::])))
'''
#遍历所有的子矩阵,四重循环
for x1 in range(1,n+1):
for y1 in range(1,m+1):
for x2 in range(x1,n+1):
for y2 in range(y1,m+1):
#注意公式
ans = sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1]
if ans <= k:
t+=1
print(t)狗屎的时间限制,但是无所谓了。你比赛你搞一个试试呢。不过按照老师的经验+资料显示,PyPy3的性能是更好的,考试中要是用到这个那真是。
差分
终于要学差分了。前缀和开了坑之后一直想学一直没学。感谢!
是什么?
相邻两个元素求差。对差分做前缀和可以得到原数组。
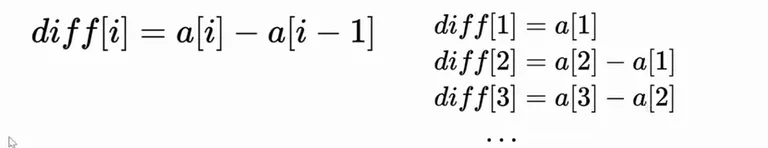
应用:区间加法
某个区间加上x,对于差分数组而言:
- 左端点加上x;
- 右端点+1 减去x。
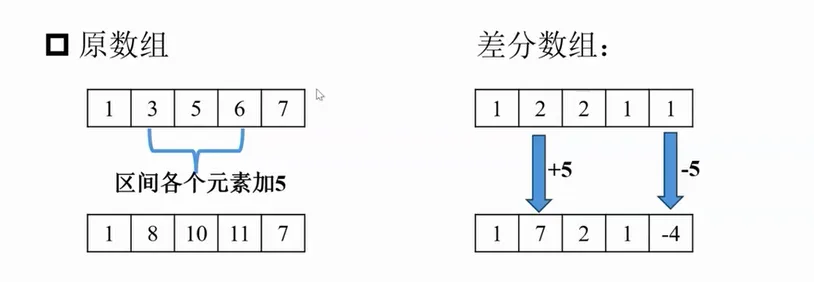
实现O(1)的区间加法。
注意事项
- 无法边修改边查询;
- diff[i]+x:从i【包括i在内】往后的所有数字+x;
- diff[i]-x:从i+1【包括i+1在内】往后的所有数字-x;
例题:区间更新
import sys
from itertools import *
input = lambda:sys.stdin.readline().strip()
n,m = map(int,input().split())
ls =[0]
ls.extend(list(map(int,input().split())))
#差分预处理
diff = [0]
for i in range(1,n+1):
diff.append(ls[i] - ls[i-1])
for i in range(m):
x,y,z = map(int,input().split())
diff[x]+=z
#这里注意要判断
if y+1 <= n:
diff[y+1]-=z
ls = list(accumulate(diff))
print(" ".join(map(str,ls[1::])))二维差分数组定义
由二维差分数组的前缀和就是原数组可以得到:
diff[i][j] = a[i][j] - a[i-1][j] - a[i][j-1] + a[i-1][j-1]得到模板如下:
import sys
input = lambda:sys.stdin.readline().strip()
n,m= map(int,input().split())
#注意下标从1开始
num = [[0] * (m+1) for i in range(n+1)]
diff= [[0] * (m+1) for i in range(n+1)]
t = 0
for i in range(1,n+1):
#num[i]表示一行数组
num[i] = [0] + list(map(int,input().split()))
#预处理从行或者从列开始都行,习惯上按行处理
for i in range(1,n+1):
for j in range(1,m+1):
diff[i][j] = num[i][j] - num[i-1][j] - num[i][j-1] + num[i-1][j-1]
for i in range(1,1+n):
print(" ".join(map(str,diff[i][1::])))案例输入:
4 4
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16输出:
1 1 1 1
4 0 0 0
4 0 0 0
4 0 0 0二维应用:给一个矩阵的数字都加上x
正对角线加,副对角线减
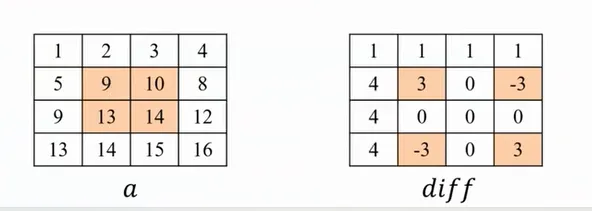
公式如下:
diff[x1][y1] +=x
diff[x2+1][y2+1] +=x
diff[x1][y2+1] -=x
diff[x2+1][y1] -=x根据之前的案例写一下:
import sys
input = lambda:sys.stdin.readline().strip()
n,m= map(int,input().split())
#注意下标从1开始
num = [[0] * (m+1) for i in range(n+1)]
diff= [[0] * (m+1) for i in range(n+1)]
ans= [[0] * (m+1) for i in range(n+1)]
t = 0
for i in range(1,n+1):
#num[i]表示一行数组
num[i] = [0] + list(map(int,input().split()))
#预处理从行或者从列开始都行,习惯上按行处理
for i in range(1,n+1):
for j in range(1,m+1):
diff[i][j] = num[i][j] - num[i-1][j] - num[i][j-1] + num[i-1][j-1]
#做一次+3
diff[2][2] +=3
diff[3+1][3+1] +=3
diff[2][3+1] -=3
diff[3+1][2] -=3
#还原
for i in range(1, n + 1):
for j in range(1, m + 1):
ans[i][j] = ans[i - 1][j] + ans[i][j - 1] - ans[i - 1][j - 1] + diff[i][j]
for i in range(1,1+n):
print(" ".join(map(str,ans[i][1::])))得到输出:
1 2 3 4
5 9 10 8
9 13 14 12
13 14 15 16离散化
定义
不关心数字本身,只关心大小关系(排名),本质上是一种哈希
eg.[100,200,300,400,500],离散化为[1,2,3,4,5]
凡是只关心排序关系的题目,均可以离散化。
步骤
- 数组拷贝;
- 副本排序并去重;
- 将原数组的元素设置为副本的下标【用到二分查找】。
学到了:二分查找的库
导入库:
from bisect import *具体函数使用:
| 函数 | 功能 |
|---|---|
| bisect_left(a, x, [lo=0, hi=len(a)]) | 在序列 a 中二分查找适合元素 x 插入的位置,即返回第一个大于等于x的位置 |
| bisect_right(a, x, [lo=0, hi=len(a)]) | 在序列 a 中二分查找适合元素 x 插入的位置,即返回第一个大于x的位置 |
编程感受:
from bisect import *
a = [5, 6, 7, 8, 9]
print(bisect_left(a,4))
print(bisect_left(a,5))
print(bisect_left(a,10))
print(bisect_right(a,4))
print(bisect_right(a,5))
print(bisect_right(a,10))输出如下:
0
0
5
0
1
5模板如下:
from bisect import *
def Discreate(a):
#拷贝,集合用于去重
b = list(set(a))
#排序
b.sort()
#转换
ans = []
for i in a:
ans.append(bisect_left(b,i))
return ans
ls = [200,0,100,300,400,100,300]
print(Discreate(ls))可以得到:
[2, 0, 1, 3, 4, 1, 3]除了使用二分查找,我们还可以用字典:
#字典
def Discreate(a):
#拷贝,集合用于去重
b = list(set(a))
#排序
b.sort()
#b中的数字与下标捆绑
dic = dict(zip(b,range(len(b))))
#转换
ans = []
for i in a:
ans.append(dic[i])
return ans
ls = [200,0,100,300,400,100,300]
print(Discreate(ls))结果一致。实际离散化可能从1开始。
贪心
定义
局部最优就是整体最优
eg.最少硬币支付问题
- 1,2,5可以,因为5>2+1;
- 1,2,4,5,6不可以,没有上述的性质。
如何判断
- 找到最优子结构:问题的最优解包含子问题的最优解,也就是大问题分解成子问题;
- 性质选择。
具体问题
- 经典贪心问题
- 举反例
经典问题
例题:石子合并问题
当下最少的策略
选择两个最小的进行合并
数据结构选择
最小堆heapq,每次获取最小的元素,这里就来学一下这个结构吧(老亡羊补牢人了)
堆:分为大根堆与小根堆,使用数组表示的二叉树。在heapq库中,heapq使用的数据类型是Python的基本数据类型list。
用到的函数如下:其中的heap都是列表类型
| 函数 | 功能 |
|---|---|
| heappush(heap,item) | 往堆中添加新值,自动建立小根堆,一般在空列表上好用 |
| heapify(heap) | 以线性时间将一个列表转化为小根堆 |
| heappop(heap) | 返回堆中的最小值 |
| nlargest(num, heap) | 从堆中取出num个数据,从最大的数据开始取,返回结果是一个列表 |
| nsmallest(num, heap) | 从堆中取出num个数据,从最小的数据开始取,返回结果是一个列表 |
| merge(sorted(array_a), sorted(array_b)) | 将两个有序的列表合并成一个新的有序列表,返回结果是一个迭代器 |
| heappushpop(heap, num) | 先将num添加到堆中,然后将堆顶的数据出堆 |
| heapreplace(heap, num) | 先将堆顶的数据出堆,然后将num添加到堆中 |
进而实现这道题目:
import sys
import heapq
input = lambda:sys.stdin.readline().strip()
n = int(input())
a = list(map(int ,input().split()))
#转换成堆
heapq.heapify(a)
ans = 0
while len(a) >= 2:
x = heapq.heappop(a)
y = heapq.heappop(a)
heapq.heappush(a,x+y)
ans += x+y
print(ans)例题:分组问题
类似:上船,船能够承载的质量一定
思路
从大的开始往前看,如果能找到合适的凑在一起,那么就凑,不能就单独为一组。
为什么可以这样遍历【为什么可以这样贪心】?如果小的不和最大最合适的配合,那么跟别的搭配,浪费的空间一定是最大的
例题:翻硬币问题
思路
为了保证最终能够翻出来,从左往右翻就行。
例题:数组乘积问题

思路
a从小到大,b从大到小,两两配对。这个可以用数学的方法证明
双指针
是什么?
进行区间操作时,利用两个下标同时遍历。
类型
- 反向扫描:相遇或者满足某些条件的时候停止扫描
有序数组、字符串
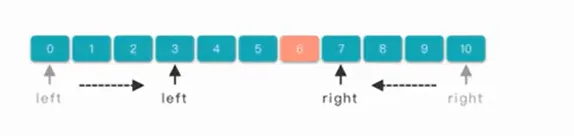
eg.分箱问题、回文字符串
s = input()- 同向扫描:也叫做滑动窗口,维护一个[left,right]的区间

- 左端点向右移动表示删除元素
- 右端点向右移动表示增加元素在尾部或者满足特殊条件时停止
例题:美丽的区间
用前缀和时间会爆掉,所以用双指针进行优化。
思路
遍历每一个左端点,右端点不断向右移动,恰好满足大于等于S的时候就是每个左端点最“美丽”的情况。
这道题能用双指针的原因就在于所有数字都是正数,有点递增的味道。
import sys
input = lambda:sys.stdin.readline().strip()
n,s = map(int,input().split())
ls = list(map(int,input().split()))
l,r = 0,0
tot = 0
length = n
#滑动窗口[l,r],r不包含在区间中,用于表示下一个要加入的数字
while l < n:
#不断扩展右端点,直至区间之和大于等于s
while r<n and tot < s:
tot += ls[r]
r+=1
#更新最美丽区间的长度,注意判断条件
if tot >= s:
length = min(length,r - l)
#更新左端点
tot -= ls[l]
l += 1
if length == n:
length = 0
print(length)例题:挑选子串
- 根据条件把数组变成01数组,用数字的和代表几个数满足。但是这种会增加时间消耗,也啥必要直接判断就行;
- 对于每个l,找到最小的r,r+1,r+2……n均为合法区间。
编程实践如下:
import sys
input = lambda:sys.stdin.readline().strip()
n,m,k = map(int , input().split())
ls = list(map(int , input().split()))
ans = 0
l,r = 0,0
tot = 0
while l < n:
while r < n and tot < k:
if ls[r] >= m:
tot += 1
r += 1
if tot >= k:
#注意这里r不包含在区间内
ans += n - r + 1
if ls[l] >= m:
tot -= 1
l += 1
print(ans)二分
是什么?
每次将搜索范围缩小一半,在O(logn)时间内找到正确答案
前提/核心
单调性
例题:手算根号2
- 在[1,2],计算1.5**2 = 2.25>2;
- 在[1,1.5],计算1.25**2 < 2; ……
编写代码如下:
l,r = 1,2
#假设要求是精确到小数点后3位,说明区间长度小于等于1e-4,或者自己限定循环次数
while r - l >= 1e-4:
mid = (l + r) / 2
#根据中点调整区间
if mid ** 2 > 2:
#调整为[l,mid]
r = mid
else:
#调整为[mid,r]
l = mid
#保留小数输出位数
print("{:.3f}".format(l))步骤
- 候选区间[l,r];
- 计算中点mid = (l+r) /2
- 判断中点是否合法,对应调整范围,循环直到区间满足特定条件。
用途
- 查找有序列表中元素x的下标;
- 浮点二分:计算根号2;
- 二分答案:求解的问题具有单调性
二分答案步骤
题目具有单调性质,采用猜答案+二分
- 确定范围[l,r],考虑最极端的情况就行;
- l <= r时:
- mid
- check(mid)
- mid合法:更新ans
- 根据合法调整区间:l = mid+1 or r = mid-1
例题:分巧克力
这里的单调性在于,巧克力的边长越长,得到的数量越少
n,k = map(int,input().split())
#保存每块巧克力的信息
a = []
#这里写成1e5会导致ans变成小数
max_num = 100000
for i in range(n):
x,y = map(int,input().split())
a.append((x,y))
#合法:边长为x,能够切出k块
def check(x):
tot = 0
for i in range(n):
#这里记得加括号
tot += (a[i][0] // x) * (a[i][1] // x)
if tot >= k :
return True
else:
return False
l,r = 1,max_num
ans = 0
while l <= r:
mid = (l+r) // 2
if check(mid):
#可以:求是不是有更大的
ans = mid
l = mid+1
else:
#不可以:缩小边长
r = mid -1
print(ans)例题:跳石头
特殊的标签:最大值最小化,最小值最大化,一般都是二分答案
至多移走M块岩石,又可知,移除的石头越多,最短跳跃距离越大,具有单调性。
因此我们对最短跳跃距离进行二分,思路是:猜最短跳跃距离为x,统计在这种情况下需要移走多少岩石。没有超过M块,就是合法的。
import sys
input = lambda:sys.stdin.readline().strip()
l,n,m = map(int ,input().split())
a = []
for i in range(n):
a.append(int(input()))
#猜最短跳跃距离为x,统计在这种情况下需要移走多少岩石。没有超过M块,就是合法的。
def check(x):
#移除的数量
tnt = 0
#last_p用于计算距离
last_p = 0
for i in range(n):
#如果这块石头跟上一块的距离小于x,移除这块石头
if a[i] - last_p < x:
tnt+=1
else:
last_p = a[i]
#终点石头特判,如果不符合就说明x不行
if l - last_p < x:
#注意这里老师讲的不对,如果最后这个不满足,直接加1,把倒数第二块石头移开就行了,因为倒数第二和倒数第三之间的距离满足大于等于x,所以不用再做别的验证
tnt+=1
#确保移除的数量小于等于m
if tnt <= m:
return True
return False
left,right = 1,l
ans = 0
while left<=right:
mid = (left+right) // 2
if check(mid):
ans = mid
left = mid+1
else:
right = mid-1
print(ans)例题:肖恩的乘法表
通读完题目之后,感觉用暴力实现是很简单的。
import sys
input = lambda:sys.stdin.readline().strip()
n,m,k = map(int , input().split())
ls = []
for i in range(1,n+1):
for j in range(1,m+1):
ls.append(i*j)
ls.sort()
print(ls[k-1])然后就时间没问题,但是全部超过内存限制了。内存在270000+kb,恰好超了内存一点点。
我们尝试一下减小内存:
import sys
input = lambda:sys.stdin.readline().strip()
n,m,k = map(int , input().split())
ls = []
for i in range(1,n+1):
for j in range(1,m+1):
ls.append(i*j)
ls.sort()
if len(ls)>k:
ls = ls[:k]
print(ls[k-1])妈的测评系统总是突然之间就尼玛炸了……但是我从测评结果进去,这么做时间又炸了……
用二分的思路,我们就是要猜第k小的数字是多少,然后看比这个数小的数字有多少个。
import sys
input = lambda:sys.stdin.readline().strip()
n,m,k = map(int , input().split())
def check(x):
cnt = 0
#第i行的数字为i,2i,3i,4i…mi
#因为i*j<=x,所以j<=x//i
for i in range(1,n+1):
#考虑m很小的情况
cnt += min(m,x//i)
return cnt
left , right=1,n*m
while left <= right:
mid = (left + right)//2
if check(mid) >= k:
#大了
#等于在哪,ans的更新就在哪
#这里更新ans是与check函数有关的,check函数统计的是小于等于该数的总数,数字有重复
ans = mid
right = mid - 1
else:
left = mid + 1
print(ans)二分答案的习题:还得练

刚才打开倍增的视频,发现居然是C++的……算了几块钱的课能看多少是多少吧。
哈希
主要就是要复习字典的使用。字典在判断一个数字是否在字典中的时间复杂度为O(1)级别。
例题:两数之和
#最终返回的是一个列表
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
dic = {}
n = len(nums)
#判断在该数之前有没有凑起来正好是target的数字
for i,x in enumerate(nums):
if dic.get(target-x) is not None:
return [i,dic[target-x]]
dic[x] = i 倍增
位运算
还要自己找一下资源,先放个坑在这里

